Geogebra

El Geogebra és un programari lliure que en l'aerea de Visual i Plàtica ens anirà bé per tractar tots aquells conceptes relacionats amb el dibuix geomètric: traçat de poligons, dibuix de corbes, enllaços, tangències...

Podem descarregar una versió instal·lable al nostre ordinador o bé usar una versió on line. Cal tenir el motor java instal·lat.

Si voleu ajuda per a fer la instal·lació aquest enllaç us pot anar bé.

enllaços:

- exemples de matemàtiques, molts d'ells de geometria plana.

- Curs D55 - Matemàtiques amb geogebra. Per a un coneixement a fons del programa

Tot seguit resoldrem aquest exercici: circumcentre, construcció i propietats

En aquesta pràtica ens proposarem:

- dibuixar un triangle

- trobar les seves rectes mediatrius

- determinar on és el circumcentre

- dibuixar la circumferència circumscrita al triangle.

- Finalment canviarem la forma del triangle i veurem com canvia el circumcentre i la circumferència circumscrita.

1.- Obrim el geogebra

2.- Si no el tenim configurat en català el podem canviar fent opciones/idioma/A-D/Catalan

3.- Donat que no ens farà falta, desactivarem els eixos: visualitza/eixos. Tampoc necessitem la finestra algebraica. La treurem fent: Visuallitza/Finestra Algebràica.

4.- A la part superior disposem de la barra de menús i davall la de grup d'eines. Per a utilitzar una eina fem clic al triangle petit de la casella corresponent al grup d'eines i seleccionem l'eina.

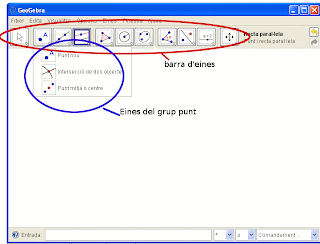
5.- Comencem dibuixant un triangle acutangle: Seleccionem polígon que està en el 5è grup d'eines. Dibuixem el triangle tot fent clic en pantalla en els vertex. Després d'assenyalar el 3r vèrtex toquem el punt inicial, d'aquesta manera completarem el triangle.

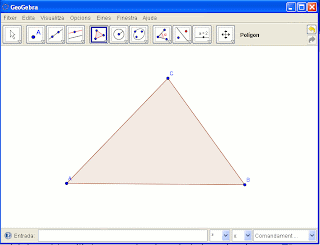
6.- Les mediatrius dels costats les podriem dibuixar manualment com ho fariem sobre el paper amb l'ajut del compàs. No obstant utilitzarem l'eina mediatriu que està en el 4t grup d'eines.

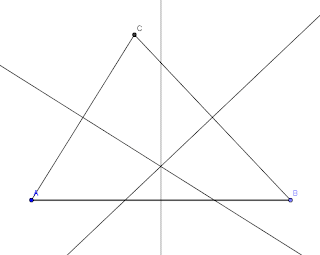
7.- Seleccionem punt intersecció de dos objectes que està en el 2n grup d'eines i assenyalarem el punt intersecció de les mediatrius. Fent clic en el nou punt amb el botó dret podrem canviar el nom del punt. Hi posarem Circumcentre.

8.- Tot seguit dibuixarem la circumferència circumscrita. Triem circumferència donats el seu centre i un punt per on pasa que està en el 6è grup d'eines. Fem clic en el circumcentre i després en un vèrtex quasevol del triangle.

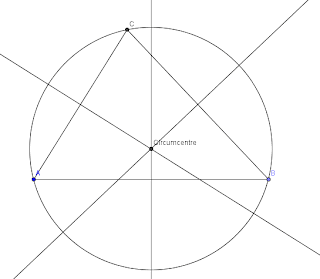
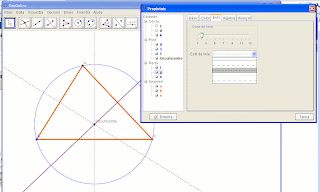
9.- Acolorirem i canviarem el format dels diferents elements.Els costats el posarem de color taronja i un gruix de 7: clic amb el botó dret damunt la línia i propietats/color triem taronja. En aquest mateix quadre en la pestanya gruix de línia desplacem el lliscador fins a 7. Finalment fem tanca. De la mateixa manera canviarem les rectes mediatrius i la circumferència.

10.- Finalment podem canviar les propietats inicials del triangle i veurem com afecte al seu circumcentre i a la circumferència circumscrita. Seleccionem l'eina Moure, la 1a de l'esquerra i arrosseguem un dels vègterx. Observarem com canvia la forma del triangle, el seu circumcentre i la circumferència circumscrita, sempre però passarà pels vèrtex del triangle.

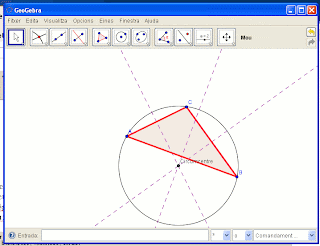
Podem fer una colla de reflexions com ara:

- El circumcentre sempre ha d'estar dins del trinagle?.

- que passa quan el circumcentre està en un costat del triangle